ವಾಸ್ತವಿಕ ಸಂಖ್ಯೆಗಳು
ವಾಸ್ತವಿಕ ಸಂಖ್ಯೆಗಳು
ನಾವೀಗಾಗಲೇ ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆಗಳು (1, 3, 7), ಪೂರ್ಣಸಂಖ್ಯೆಗಳು (0,1,3,7), ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳು (1/2, -6/5 ),
ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳು ( , )ಇವುಗಳ ಗುಣಲಕ್ಷಣಗಳನ್ನು ಕಲಿತಿದ್ದೇವೆ. ಅಲ್ಲದೆ, ಗುಣಾಕಾರದ ಮತ್ತು ಸಂಕಲನದ ವಿಲೋಮಗಳನ್ನು ತಿಳಿದಿದ್ದೇವೆ
ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳು ಮತ್ತು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳು ಇವುಗಳನ್ನು ಒಟ್ಟಾಗಿ ವಾಸ್ತವಿಕ ಸಂಖ್ಯಾಗಣ (real number set) ಎನ್ನುತ್ತೇವೆ ಮತ್ತು ‘R’ ಸಂಕೇತದಿಂದ ಸೂಚಿಸುತ್ತೇವೆ. ಯಾವುದೇ ಒಂದು ಸಂಖ್ಯೆಯು ಒಂದೋ ಭಾಗಲಬ್ಧ, ಇಲ್ಲವೇ ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಯಾಗಿರಬಹುದು. ಒಂದೇ ಸಂಖ್ಯೆ ಎರಡೂ ಆಗಲು ಸಾಧ್ಯವಿಲ್ಲ. R Ir = ಶೂನ್ಯಗಣ)
N : ಸ್ವಾಭಾವಿಕ ಸಂಖ್ಯೆಗಳ ಗಣ, W : ಪೂರ್ಣ ಸಂಖ್ಯೆಗಳ ಗಣ, Z : ಪೂರ್ಣಾಂಕಗಳ ಗಣ, Q : ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳ ಗಣ, R : ವಾಸ್ತವಿಕ ಸಂಖ್ಯೆಗಳ ಗಣ, Ir : ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳ ಗಣ ಆದರೆ, ಈ ಸಂಖ್ಯಾಗಣಗಳಿಗಿರುವ ಸಂಬಂಧವನ್ನು ಕೆಳಗಿನ ವೃಕ್ಷನಕ್ಷೆಯಲ್ಲಿ ಸೂಚಿಸಬಹುದು.
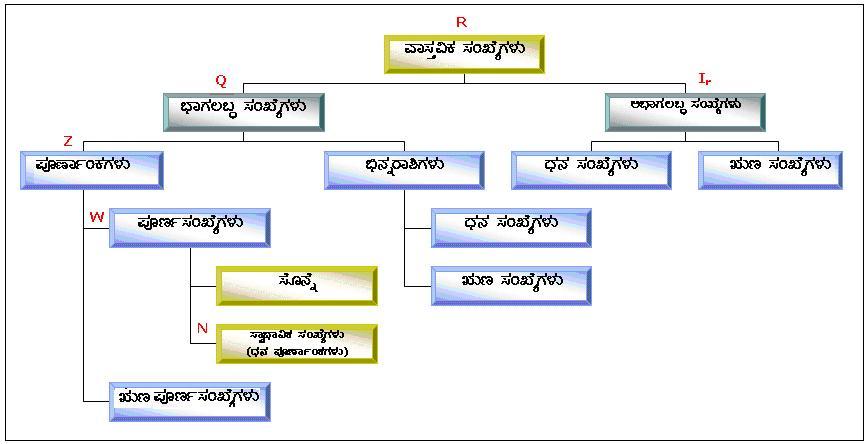
ಈ ಮೇಲಿನ ಸಂಬಂಧವನ್ನು ವೆನ್ ನಕ್ಷೆಯ ಮೂಲಕ ಕೂಡಾ ಪ್ರತಿನಿಧಿಸಬಹುದು:
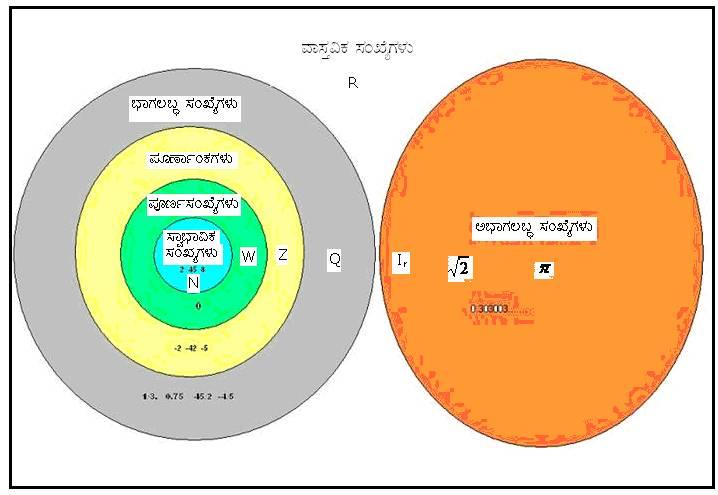
a, b, c R. ಇಲ್ಲಿ è R ಎಂಬುದು ವಾಸ್ತವಿಕ ಸಂಖ್ಯಾಗಣ ಆದರೆ,
|
ಸಂ. |
ಸಂಬಂಧ |
ಲಕ್ಷಣದ ಹೆಸರು |
|
1 |
a=a |
ಸ್ವತೋಲನ ಗುಣಧರ್ಮ |
|
2 |
a=b ಆದರೆ b=a |
ಸಮಮಿತಿಯ ಗುಣಧರ್ಮ |
|
3 |
a=b, b=c ಆದರೆ a=c |
ಸಂಕ್ರಮಕ ಸಂಬಂಧ |
|
4 |
a=b ಆದರೆ a+c =b+c, ac=bc |
|
|
5 |
ac=bc, c 0 ಆದರೆ a=b |
|
|
6 |
a+b R |
ಸಂಕಲನದ ಆವೃತಗುಣ |
|
7 |
a-b R |
ವ್ಯವಕಲನದ ಆವೃತ ಗುಣ |
|
8 |
a*b R |
ಗುಣಾಕಾರದ ಆವೃತ ಗುಣ |
|
9 |
a/b R, b 0 ಆದಾಗ |
ಭಾಗಾಕಾರದ ಆವೃತ ಗುಣ |
|
10 |
a+b = b+a |
ಸಂಕಲನದ ಪರಿವರ್ತನೀಯ ಗುಣ |
|
11 |
a*b = b*a |
ಗುಣಾಕಾರದ ಪರಿವರ್ತನೀಯ ಗುಣ |
|
12 |
(a+b)+c = a+(b+c) |
ಸಂಕಲನದ ಸಹವರ್ತನೀಯ ಗುಣ |
|
13 |
a*(b*c) = (a*b)*c |
ಗುಣಾಕಾರದ ಸಹವರ್ತನೀಯ ಗುಣ |
|
14 |
a*(b+c) = a*b + a*c, (b+c)*a = b*a+c*a |
ವಿಭಾಜಕ ನಿಯಮ |
|
15 |
a+0 =0+a =a |
0 ಯು ಸಂಕಲನದ ಅನನ್ಯತಾಂಶ |
|
16 |
a*1= 1*a=a |
1 ಗುಣಾಕಾರದ ಅನನ್ಯತಾಂಶ |
|
17 |
a+ (-a) = 0 |
-a ಯು ‘a’ ಯ ಸಂಕಲನದ ವಿಲೋಮ |
|
18 |
a*1/a =1 --> a 0 ಆದಾಗ, |
1/aಯು ಎಲ್ಲಾ ‘a’ ಚಿ’ಗಳ ಗುಣಾಕಾರದ ವಿಲೋಮ |
a, b ಮತ್ತು c ಗಳು ವಾಸ್ತವ ಸಂಖ್ಯೆಗಳಾದರೆ :
|
1 |
|
a=b ಅಥವಾ a<b ಅಥವಾ a>b |
|
2 |
a <b ಆದರೆ |
ಆಗ b>a |
|
3 |
a<b ಮತ್ತು b <c ಆದರೆ |
ಆಗ a<c |
|
4 |
a<b ಮತ್ತು c ಯು ಸೊನ್ನೆ ಆಗದೇ ಇರುವಾಗ |
ಆಗ a+c < b+c |
|
5 |
a<b ಆಗಿದ್ದಲ್ಲಿ |
ಮತ್ತು c>0 ಆದರೆ ಆಗ ac< bc |
|
ಮತ್ತು c<0 ಆದರೆ ac > bc |
ಸಮಸ್ಯೆ 1: ಬಿಡಿಸಿ (x-3)/x2+4 >= 5/x2+4
ಪರಿಹಾರ:
ಬಿಡಿಸುವುದು ಎಂದರೆ x ನ ಬೆಲೆಯನ್ನು ಕಂಡುಹಿಡಿಯುವುದು.
ಎರಡೂ ಬದಿಯನ್ನು x2+4 ನಿಂದ ಗುಣಿಸಿದಾಗ
(x-3)>= 5( x2+4 >0)
x >=5+3 (3 ನ್ನು ಎರಡೂ ಕಡೆ ಕೂಡಿಸಿದಾಗ )
x >=8
ತಾಳೆ : x =8,9 ನೀಡಿ ಪರೀಕ್ಷಿಸಿ .
ಯೂಕ್ಲಿಡ್ ನ ಅನುಪ್ರಮೇಯ
ಅನುಪ್ರಮೇಯವು ಒಂದು ಸಾಧಿಸಲಾಗದ ಹೇಳಿಕೆಯಾಗಿದ್ದು ಇನ್ನೊಂದು ಹೇಳಿಕೆಯನ್ನು ಸಾಧಿಸಲು ಸಹಾಯ ಮಾಡುತ್ತದೆ.
ನಮಗೆ ತಿಳಿದಿರುವಂತೆ
ಭಾಜ್ಯ = (ಭಾಜಕ*ಭಾಗಲಬ್ಧ)+ಶೇಷ, (ಇಲ್ಲಿ 0 ಶೇಷ < ಭಾಜಕ)
ಈ ಸಂಬಂಧವನ್ನು ಯೂಕ್ಲಿಡ್ ನ ಭಾಗಾಕಾರದ ಅನುಪ್ರಮೇಯ ಎಂದು ಕರೆಯುತ್ತೇವೆ.
ಇದನ್ನು ಇನ್ನೊಂದು ರೀತಿಯಲ್ಲಿ ಹೇಳುವುದಾದರೆ ಯಾವುದೇ ಎರಡು a ಮತ್ತು b ಧನಪೂರ್ಣಾಂಕಗಳಾಗಿದ್ದಾಗ ಎರಡು q ಮತ್ತು r ಎನ್ನುವ ಅದ್ವಿತೀಯ ಪೂರ್ಣಾಂಕಗಳು a=b*q+r ಎನ್ನುವ ಸಂಬಂಧವನ್ನು ಹೊಂದಿರುತ್ತವೆ ಮತ್ತು
0 r<b ಆಗಿರುತ್ತದೆ.
ನಾವು ಈಗಾಗಲೇ ಭಾಗಾಕಾರ ಮತ್ತು ಅಪವರ್ತನ ವಿಧಾನದಿಂದ ಮ.ಸಾ.ಅ. ವನ್ನು ಕಂಡುಹಿಡಿಯಲು ಕಲಿತಿದ್ದೇವೆ
ಯೂಕ್ಲಿಡ್ ನ ಭಾಗಾಕಾರದ ಅನುಪ್ರಮೇಯವನ್ನು ಉಪಯೋಗಿಸಿಯೂ ಮ.ಸಾ.ಅ. ಕಂಡುಹಿಡಿಯಬಹುದು
ಈ ವಿಧಾನದಲ್ಲಿ ಚಿಕ್ಕ ಸಂಖ್ಯೆಯನ್ನು ಮೊದಲ ಭಾಜಕವಾಗಿ ಆರಂಭಿಸಿ ತದನಂತರ ಆ ಹಂತದ ಭಾಜಕವನ್ನು ಆ ಹಂತದ ಶೇಷದಿಂದ ಭಾಗಿಸುತ್ತಾ ಹೋಗುತ್ತೇವೆ. ಶೇಷ ಸೊನ್ನೆಯಾಗುವ ಹಂತದಲ್ಲಿರುವ ಭಾಜಕವೇ ಮ.ಸಾ.ಅ.
ಸಮಸ್ಯೆ 2: 305 ಮತ್ತು 793 ಗಳ ಮ.ಸಾ.ಅ. ಕಂಡುಹಿಡಿಯಿರಿ
ಪರಿಹಾರ:
|
ಭಾಜಕ |
ಭಾಗಾಕಾರ |
ಭಾಗಲಬ್ಧ |
ಶೇಷ |
|
305 |
305)793(2 610 |
2 |
183 |
|
183 |
183)305(1 183 |
91 |
122 |
|
122 |
122)183(1 122 |
1 |
61 |
|
61 |
61)122(1 122 |
2 |
0 |
305 ಮತ್ತು 793 ಗಳ ಮ.ಸಾ.ಅ. 61.
ಸಮಸ್ಯೆ 3: ಒಂದು ಆಯತಾಕಾರದ ಹೊಲದ ಉದ್ದ 110m ಮತ್ತು ಅಗಲ 30m. ಉದ್ದ ಮತ್ತು ಅಗಲಗಳೆರಡನ್ನು ನಿಖರವಾಗಿ ಅಳತೆ ಮಾಡುವ ಗರಿಷ್ಠ ಉದ್ದದ ಸಲಾಕೆಯ ಉದ್ದ ಎಷ್ಟು?
ಪರಿಹಾರ:
|
ಭಾಜಕ |
ಭಾಗಾಕಾರ |
ಭಾಗಲಬ್ಧ |
ಶೇಷ |
|
30 |
30)110(3 90 |
3 |
20 |
|
20 |
20)30(1 20 |
1 |
10 |
|
10 |
10)20(2 20 |
2 |
0 |
110 ಮತ್ತು 30 ಗಳ ಮ.ಸಾ.ಅ. 10.
10M ಉದ್ದವಿರುವ ಸಲಾಕೆಯಿಂದ ಹೊಲದ ಉದ್ದ ಮತ್ತು ಅಗಲವನ್ನು ನಿಖರವಾಗಿ ಅಳೆಯಬಹುದು.
ಅವಿಭಾಜ್ಯವಾದ 1 ಕ್ಕಿಂತ ದೊಡ್ಡ ಸಂಖ್ಯೆಯನ್ನು ಸಂಯುಕ್ತಸಂಖ್ಯೆ(composite number) ಎಂದು ಕರೆಯುತ್ತೇವೆ.
ಗಮನಿಸಿ 24= 2*2*2*3= 3*2*2*2 ಮತ್ತು 55=11*5= 5*11
ಯಾವುದೇ ಸಂಖ್ಯೆಯನ್ನು ಎರಡು ಅವಿಭಾಜ್ಯ ಸಂಖ್ಯೆಗಳ ಗುಣಲಬ್ಧವಾಗಿ ಅದ್ವಿತೀಯ ರೀತಿಯಲ್ಲಿ ವ್ಯಕ್ತಪಡಿಸಬಹುದು. ಇದನ್ನು ಅಂಕಗಣಿತದ ಮೂಲ ಪ್ರಮೇಯ(fundamental theorem) ಎಂದು ಕರೆಯುತ್ತೇವೆ.
ಸಮಸ್ಯೆ 3: 18,81 ಮತ್ತು 108 ಗಳ ಮ.ಸಾ.ಅ. ಮತ್ತು ಲ,ಸಾ.ಅ. ಕಂಡುಹಿಡಿಯಿರಿ
ಪರಿಹಾರ:
18=2*9= 2*32
81=9*9=34
108 = 12*9 = 4*3*9 = 22*33
ಮ.ಸಾ.ಅ = 32=9
ಲ.ಸಾ.ಅ.= 22*34= 4*81= 324
3 ಸಂಖ್ಯೆಗಳ ಮ.ಸಾ.ಅ * ಲ.ಸಾ.ಅ. 3 ಸಂಖ್ಯೆಗಳ ಗುಣಲಬ್ಧ
ಪ್ರಮೇಯ: a ಯು 1 ಕ್ಕಿಂತ ಜಾಸ್ತಿಯಾಗಿರುವ ಪೂರ್ಣಾಂಕವಾಗಿರುವಾಗ, ಒಂದು ಅವಿಭಾಜಿತ ಸಂಖ್ಯೆ p ಯು a2 ನ್ನು ಭಾಗಿಸಿದರೆ p ಯು a ಯನ್ನು ಭಾಗಿಸುತ್ತದೆ
ಸಾಧನೆ : a ನ ಅಪವರ್ತನಗಳು p1,p2,p3, … ,pn ಆಗಿರುವಾಗ a = p1*p2*p3* … *pn
ಎರಡೂ ಕಡೆ ವರ್ಗಗೊಳಿಸುವುದರಿಂದ
a2=( p1*p2*p3* … *pn)2
p ಯು a2 ನ್ನು ಭಾಗಿಸುತ್ತದೆ ಎಂದು ಕೊಟ್ಟಿರುವುದರಿಂದ p ಯು p12*p22*p32* … *pn2 ಗಳ ಒಂದು ಅಪವರ್ತನವಾಗಿರುತ್ತದೆ
p ಯು p1,p2,p3, … ,pn ಗಳಲ್ಲಿ ಒಂದು ಆಗಿರಲೇ ಬೇಕು .
ಅಂದರೆ p ಯು a ಯನ್ನು ಭಾಗಿಸುತ್ತದೆ
1.6 ಸಮಸ್ಯೆ 3: p ಯು ಒಂದು ಅವಿಭಾಜ್ಯ ಪೂರ್ಣಾಂಕವಾಗಿದ್ದಲ್ಲಿ , ಯು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ತೋರಿಸಿ
ಪರಿಹಾರ:
ಒಂದು ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ಎಂದು ಊಹಿಸಿ ಆಗ = a/b(a, b ಗಳು ಪೂರ್ಣಾಂಕಗಳು ಸುಲಭೀಕರಿಸಿದ ರೂಪದಲ್ಲಿ )
pb2= a2=( p1*p2*p3* … *pn)2 ಇಲ್ಲಿ p1,p2,p3, … ,pn ಗಳು a ನ ಅವಿಭಾಜ್ಯ ಅಪವರ್ತನಗಳು.
ಅಂದರೆ p ಯು a ಯನ್ನು ಭಾಗಿಸುತ್ತದೆ (p ಯು a ಯ ಅಪವರ್ತನ), ಆದುದರಿಂದ ಯಾವುದೋ ಒಂದು k ಯ ಬೆಲೆಗೆ a=kp
pb2=k2p2
b2= k2p
p ಯು b ಯ ಅಪವರ್ತನ
ಹಿಂದಿನ ಹಂತದಲ್ಲಿ p ಯು a ಯ ಅಪವರ್ತನ ಎಂದು ಸಾಧಿಸಿದ್ದೇವೆ ಮತ್ತೆ ಈಗ p ಯು b ಯ ಅಪವರ್ತನ ಎಂದೂ ಸಾಧಿಸಿದ್ದೇವೆ. ಅಂದರೆ p ಯು a ಮತ್ತು b ಎರಡನ್ನೂ ಭಾಗಿಸುತ್ತವೆ ಎಂದು ಸಾಧಿಸಿದ ಹಾಗಾಯಿತು.
a/b ಸುಲಭೀಕರಿಸಿದ ರೂಪದಲ್ಲಿ ಇರುವುದರಿಂದ ಇದು ಸಾಧ್ಯವಿಲ್ಲ. ಅಂದರೆ ನಮ್ಮ ಊಹೆ ತಪ್ಪು. ಆದುದರಿಂದ ಯು ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ
ಗಮನಿಸಿ:
ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ + ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ = ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ ( ಉದಾ: 3+ )
ಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ * ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ = ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆ (ಉದಾ: 4 )
ಮೂಲ : ಫ್ರೀ ಗಣಿತ
ಕೊನೆಯ ಮಾರ್ಪಾಟು : 6/5/2020
ಅಭಾಗಲಬ್ಧ ಸಂಖ್ಯೆಗಳು
